Getting Started

The GP 2 compiler translates a GP 2 program into executable C code. The generated code is executable with the support of the GP 2 library. There are several ways to set it up. For Ubuntu, the .deb package is recommended. You can also build the compiler using make. However, the setup process is not guaranteed to be stable on all Linux machines, or on machines running MacOS or Windows. We therefore provide an installation via Docker as an alternative for Linux and MacOS.

Installation

To run the compiler, you need to install the C library Judy which you may find in your distribution’s package manager. In the Ubuntu repositories, you can find it under libjudy-dev. You also need to install cmake.

There are several ways to install the compiler:

• .deb Package - This is the recommended (and a common) installation method for Ubuntu users. Advantage: easy to install by opening the file in “Software Install” or run the command sudo apt install ./gp2c.deb in the folder containing the .deb file. Disadantage: may not work on non-Ubuntu distributions.
• Pre-built - Use a version of the compiler that has already been built. This may work on non-Ubuntu distributions.
• Build from source code - Follow the link for a guide on how to build the compiler yourself.
• Docker - Follow the link for instructions on how to install the compiler via Docker. This method is recommended for MacOS users.
• University of York - In the Department of Computer Science, the compiler is installed on most Linux machines.

Usage

Usage depends on which installation method you used:

• .deb Package - usage guide
• Pre-built - bash file usage
• Build from source code - usage guide, bash file usage
• Docker - bash file usage
• University of York - usage guide

Example: Editing, Compiling, and Running a Transitive Closure Program

For this section, we assume that we can run GP 2 programs with using the command gp2c <program_file> <graph_file>.

The program we’ll look at is this:

This program computes the transitive closure of a graph. The transitive closure of a graph is the smallest extension of that graph that is transitive. A graph is transitive when for every pair of nodes v1, v2 with a path from v1 to v2, there is an edge directly from v1 to v2.

For example, this graph is not transitive:

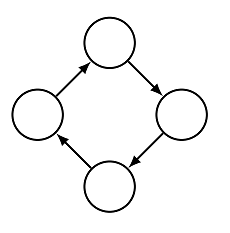
There is a path from the left-most node to the right-most node but there is no edge directly from the left-most node to the right-most node. The purpose of the program we’re looking at is the transform this graph into the smallest extension of this graph which is transitive.

Firstly, let’s get this graph in a usable form. Try writing the graph out as:

[
	(0, empty)
	(1, empty)
	(2, empty)
	(3, empty)
	|
	(4, 0, 1, empty)
	(5, 1, 2, empty)
	(6, 2, 3, empty)
	(7, 3, 0, empty)
]

What does this mean? Well the square brackets [ ... ] surround the entire graph’s structure. Then the nodes are listed, for example; (0, empty) indicates that there is a node which we will identify as node 0 and this node is unlabelled (its label is ‘empty’). After the nodes are listed, there is a divider; |, and then edges are listed. The edge (4, 0, 1, empty) describes an edge from node 0 to node 1 which is also unlabelled.

Save this graph as “cycle.host”.

Try writing this program out in text form:

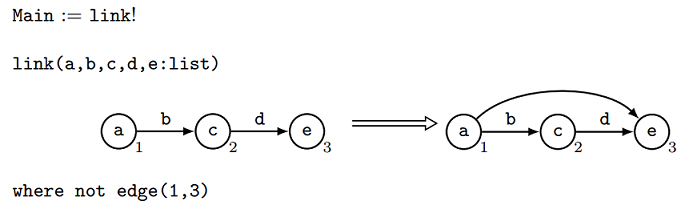
Main = link!

link(a, b, c, d, e : list)
[
	(n1, a)
	(n2, c)
	(n3, e)
	|
	(e1, n1, n2, b)
	(e2, n2, n3, d)
]
=>
[
	(n1, a)
	(n2, c)
	(n3, e)
	|
	(e1, n1, n2, b)
	(e2, n2, n3, d)
	(e3, n1, n3, empty)
]
interface = 
{
	n1, n2, n3
}
where not edge(n1, n3)

and saving it as “transitive_closure.gp2”. The general form of a program in text form is:

Main = [PROGRAM CODE]

[RULE 1]
[RULE 2]
[RULE 3]

And an individual rule is of the form:

[RULENAME]
(
	[VARIABLES]
)
[LEFT HAND SIDE GRAPH]
=>
[RIGHT HAND SIDE GRAPH]
interface = { [INTERFACE] }
[CONDITION]

Where graphs are of the same form as the graph we saw earlier.

So what does our program mean? The only line of the main program is Main = link!. This ! means that the rule link will be applied as long as possible - e.g. it will be applied until it is no longer applicable. Applying the rule link firstly searches for a match for its left hand side; 3 adjacent nodes where there is not an edge from the 1st node to the 3rd node. Then, once a match is found, the left hand side is transformed into the right hand side by inserting an edge from the 1st node to the 3rd node. The ‘interface’ describes which nodes survive; none of the 3 matched nodes n1, n2, n3 are deleted.

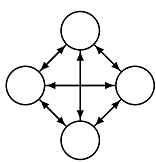
Now we can compile our program by calling:

gp2c PATH/TO/transitive_closure.gp2 PATH/TO/cycle.host

This will output the following graph:

License

See the file LICENSE.

Authors

The GP 2 language was designed by Detlef Plump.

The GP 2 compiler and runtime library was developed by Christopher Bak. Recent improvements to the compiler were implemented by Graham Campbell and Jack Romo.